ResNets

I recently found a paper regarding time-series forecasting: N-BEATS and found myself missing a few pre-requsite concept. One of them was the use of classic residual network algorithm, first proposed as ResNets. Here are some of my learning notes:

A residual neural network (ResNet) is a deep neural netword architecture, which uses skip connections/shortcuts to jump over some layers (usually 2-3 layer skips) to avoid the problems of:

1) vanishing/exploding gradients: gradients becoming too small or big when increasing layers, and
2) degradation: deeper NN has larger training/testing error.

ResNets contain typical NN characteristics of adding nonlinearities (ReLU) and batch normalization in between the layers. Note that the residual (\(F(x)\)) of a residual block will be add to an identity matrix (\(x\)) before passing on to the ReLU activation function.

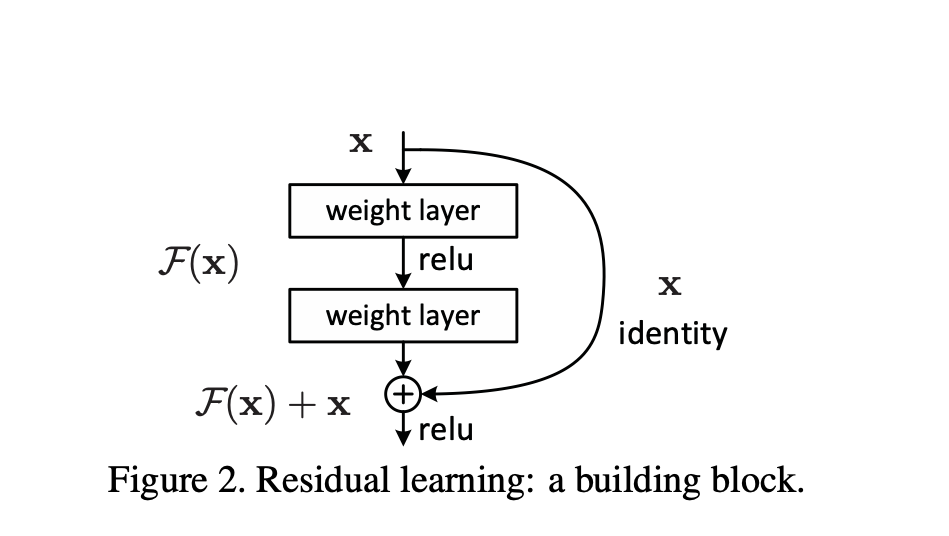
Why it solves the 2 problems above?

If considering a NN above, then \(F(x) + x = a^{[2]} = g(z^{[2]} + x) = g(w^{[2]} a^{[1]} + b^{[2]} + x)\).
To solve the above equation by minimizing \(F(x)\) as 0, we’d get \(a^{[2]} = x \approx g(x)\), where we expect \(w^{[2]} \approx 0\) and \(b^{[2]} \approx 0\) so as \(w^{[l]}\) and \(b^{[l]}\) at earlier layers (l).

Example pytorch resource for ResNet18 is here

Original ResNets paper is here.

Helpful videos & blogs:

ResNets and Why ResNets work by DeepLearningAI