RNN/LSTM

October 07, 2022

2022   ·   review     ·   dl   sequence  

My notes from reviewing RNN model in NLP, following the flow of RNN and Seq2seq lecture notes.

RNN architecture

I’ll use the below figure cited from CS224n lecture 5-6 notes of RNN to summarize RNN:

“The elements (e.g. words) were fed into the algorithm one after one along (e.g. the \(t^{th}\) element of the input sequence, \(w_{t}\)) with the hidden output layer (\(h_{t-1}\)) from the previous timestamp (\(t-1\)) in predicting the most likely next element of the output sequence (\(y_{t}\))”

\[\begin{align*} h_t & = \sigma(W^{(hh)}h_{t−1} + W^{(hx)}x_{t})\\ y_t & = \text{softmax}(W^{(S)}h_t) \end{align*}\]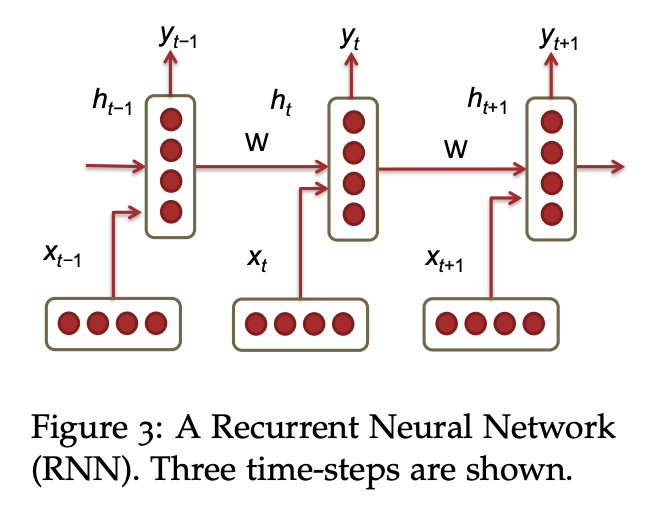
  • Parameters to be solved: \(h_t\), \(W^{(hh)}\), \(W^{(hx)}\) and \(W^{(S)}\)
  • With the softmax activation function, the common loss function for RNN is the cross-entropy loss (as derived previously in the SGD post with logistic regression):
\[\begin{align*} J^{(t)}(\theta) &= −\Sigma_{j=1}^{|V|}y_{t,j} * log(\hat{y}_{t,j}) \\ J(\theta) &= \frac{1}{T}\Sigma_{t=1}^TJ^{(t)}(\theta) \end{align*}\]
  • As the sequence is getting longer, there could be vanishing/exploding gradient problem. As we’d solve for the gradient for \(J^{(t)}(\theta)\) with chain rule with respect to multiple layers of t. The gradient can become very small or large. One way to solve the exploding gradient problem is to setup a threshold for the gradient, as the gradient exceeds the threshold, adjust the gradient to a smaller level.
  • Evaluation method of RNN model: Perplexity! The lower the perplexity, the better the model.
\[\begin{align*} \text{perplexity} = \exp({J}) \end{align*}\]

Long Short Term Memory (LSTM)

Here is a very nicely written blog and where I referenced the below figure, but I’d take my own notes below:

“LSTM is a special form of RNN that aimed to avoid the long-term dependency problem due to long sequence.”

\[\begin{align*} \color{Cerulean}\text{forget gate: } & \color{Cerulean}\boxed{f^{(t)} = \sigma(W_fh_{t−1} + U_fx_{t} + b_f)}\\ &\color{Cerulean}\textnormal{what content from t-1 is kept, $f^{(t)}$ is between 0 and 1; larger means "memory keeping"}\\ \color{blue}\text{input gate: } & \color{blue}\boxed{i^{(t)} = \sigma(W_fi_{t−1} + U_ix_{t} + b_i)}\\ \color{darkblue}\text{output gate: } & \color{darkblue}\boxed{o^{(t)} = \sigma(W_fo_{t−1} + U_ox_{t} + b_0)}\\ \\ \color{Lavender} \text{new cell content: } & \color{Lavender}\boxed{\tilde{c}_{t} = \tanh(W_ch_{t-1} + U_cx_{t} + b_c)}\\ \color{Purple} \text{new cell state: } & \color{Purple}\boxed{c_{t} = f_{t} \cdot c_{t-1} + i_t \cdot \tilde{c}_{t}} \\ &\color{Purple}\textnormal{new and carryover contents to be written}\\ \\ & h_t = o_t \cdot \tanh c_t\\ &\textnormal{new memory to be ouput}\\ \end{align*}\]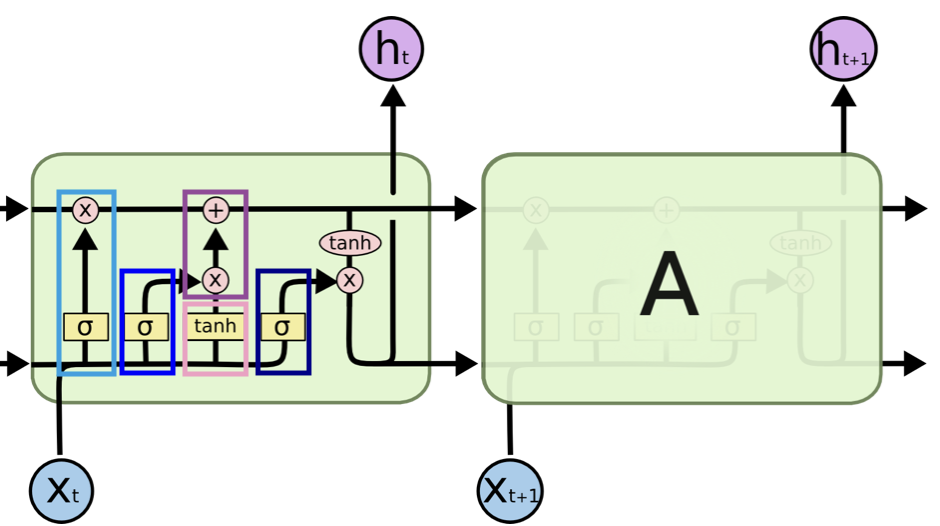

Nice RNN resources: