Monte Carlo simulation

A question that I read today: “How to estimate \(\pi\)?”

You’d find the thorough overview in the above link (and maybe a lot more blogs available online). I also gave my brain a little exercise today:

We can leverage MC simulation!

This is a very straight-forward method that everyone might come up with. As shown below, we know that the relative ratio of the areas of a circle with radius (\(r\)) and a square of width (\(2r\)) can be expressed like:

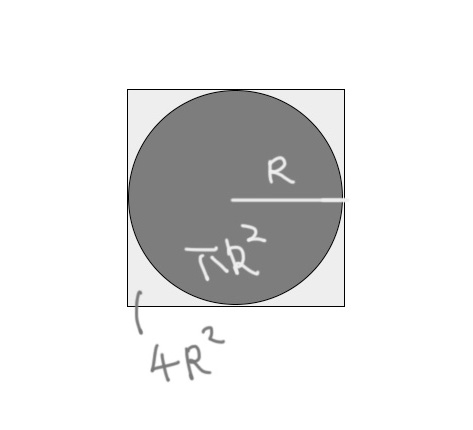
Therefore, on the Cartesian coordinate, if we can sample N samples of (x, y) pairs uniformly from the square and to keep track of the common samples that also fell into the circle (threshold: \(x^2 + y^2 < R^2\)), we can estimate \(\pi\) as:

\(\hat{\pi} = 4 \times \frac{\text{# of common samples also appears in the circle}}{\text{# of samples in the square}}\). Here is part of my sample codes:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
 
 
R = 1
N = 1000

def estimate_pi(R, N):
    """
    Estimate pi from simulation from circle
    N: Number of simulation/samples
    R: radius of the circle
    """
    
    x = np.random.uniform(-R, R, N)
    y = np.random.uniform(-R, R, N)
    in_circle = x**2 + y**2

    circle_count = 0
    for i in range(N):
        if in_circle[i] < R**2:
            circle_count += 1

    pi_hat = 4 * circle_count / N
    
    return pi_hat
 

Example notebook with above example can be found here.